论文链接:Multi Type Mean Field Reinforcement Learning, AAMAS 2020
一、问题
汪军老师组的MFQ依赖于一个重要的假设,即环境中所有的智能体均具有相同的目标,采取相似的策略。然而实际中智能体可能会多种多样,无法把它们聚合到同一个平均场中。这种场景有两种:
- 提前知道有哪些分组以及每个智能体所属的分组,如多党选举中的每个人
- 不知道智能体的分组,需要通过环境、奖励、动作来学习,如股票交易市场中的人可以分为激进型和保守型 本文针对这两种类型的场景,利用平均场论进行了方法设计。
二、解法
假设环境中的智能体可以被分为$M$类,Q函数根据智能体的划分,被分解到$X^{j}$个子集中,则Q函数可以写作如下形式: \(Q^{j}(s, a)=\frac{1}{X^{j}} \sum_{i=1}^{X^{j}}\left[Q^{j}\left(s, a^{j}, a_{1}^{k_{i}}, a_{2}^{k_{i}}, \cdots, a_{M}^{k_{i}}\right)\right]\) 其中共有$M$个类型,而$a_{m}^{k}$表示在智能体$j$的邻域中属于$m$类型的智能体$k$的动作。
2.1 Mean Field Approximation
在智能体$j$的邻域中属于$m$类型的智能体$k$的one-hot动作可以表示为$a_{m}^{k_{m}}=\bar{a}_{m}^{j}+\hat{\delta}^{j, k_{m}}$,其中$\bar{a}_{m}^{j}$为智能体$j$邻域中的所有属于类型$m$的智能体的平均作用,$\hat{\delta}^{j, k_{m}}$是单个智能体的作用与其所属类型的平均作用之间的偏差。
假设$\delta^{j, k_{i}}=\left[\hat{\delta}^{j, k_{1}} ; \hat{\delta}^{j, k_{2}} ; \cdots ; \hat{\delta}^{j, k_{M}}\right]$令为一个向量,该向量是通过将所有$M$类智能体(单个子集中的所有智能体)中智能体$j$的所有此类偏差的串联所获得的。对Q函数使用泰勒展开,可得
\[\begin{array}{l} Q^{j}(s, \mathbf{a})=\frac{1}{X^{j}} \sum_{i=1}^{X^{j}} Q^{j}\left(s, a^{j}, a_{1}^{k_{i}}, a_{2}^{k_{i}}, \cdots, a_{M}^{k_{i}}\right) \\ =\frac{1}{X^{j}} \sum_{i=1}^{X^{j}}\left[Q^{j}\left(s, a^{j}, \bar{a}_{1}^{j}, \ldots, \bar{a}_{M}^{j}\right)\right. \\ \quad+\nabla_{\bar{a}_{1}^{j}, \ldots, \bar{a}_{M}^{j}} Q^{j}\left(s, a^{j}, \bar{a}_{1}^{j}, \cdots, \bar{a}_{M}^{j}\right) \cdot \delta^{j, k_{i}} \\ \left.\quad+\frac{1}{2} \delta^{j, k_{i}} \cdot \nabla_{\tilde{a}_{1}^{j}, \ldots, \tilde{a}_{M}^{j}}^{2} Q^{j}\left(s, a^{j}, \tilde{a}_{1}^{j}, \ldots, \tilde{a}_{M}^{j}\right) \cdot \delta^{j, k_{i}}\right] \\ =Q^{j}\left(s, a^{j}, \bar{a}_{1}^{j}, \cdots, \bar{a}_{M}^{j}\right) \\ \quad+\nabla_{\bar{a}_{1}^{j}, \ldots, \bar{a}_{M}^{j}} Q^{j}\left(s, a^{j}, \bar{a}_{1}^{j}, \bar{a}_{2}^{j}, \ldots \bar{a}_{M}^{j}\right) \cdot\left[\frac{1}{X^{j}} \sum_{i=1}^{X^{j}} \delta^{j, k_{i}}\right] \\ \quad+\frac{1}{2 X^{j}} \sum_{i=1}^{j}\left[\delta^{j, k_{i}} \cdot \nabla_{\tilde{a}_{1}^{j}, \ldots, \tilde{a}_{M}^{j}}^{2} Q^{j}\left(s, a^{j}, \tilde{a}_{1}^{j}, \tilde{a}_{2}^{j}, \ldots \tilde{a}_{M}^{j}\right) \cdot \delta^{j, k_{i}}\right] \\ =Q^{j}\left(s, a^{j}, \bar{a}_{1}^{j}, \ldots, \bar{a}_{M}^{j}\right)+\frac{1}{2 X^{j}} \sum_{i=1}^{X}\left[R_{s, a^{j}}^{j}\left(a^{k_{i}}\right)\right] \approx Q^{j}\left(s, a^{j}, \bar{a}_{1}^{j}, \ldots, \bar{a}_{M}^{j}\right) \end{array}\]忽略余项,可得:
\[Q^{j}(s, \mathbf{a}) \approx Q_{M T M F}^{j}\left(s, a^{j}, \bar{a}_{1}^{j}, \ldots, \bar{a}_{M}^{j}\right)\]我们可以使用平均偏差$\sum_{k}\left|\hat{\delta}_{k}\right|_{2} / N$来评估平均场近似的效用。下面的定理证明了平均偏差会随着智能体类型的增加而减少,衡量了平均场近似误差的bound:




2.2 Mean Field Update
该Q函数的更新与使用如下:
\(Q_{t+1}^{j}\left(s, a^{j}, \bar{a}_{1}^{j}, \bar{a}_{2}^{j}, \ldots \bar{a}_{M}^{j}\right)=(1-\alpha) Q_{t}^{j}\left(s, a^{j}, \bar{a}_{1}^{j}, \bar{a}_{2}^{j}, \ldots \bar{a}_{M}^{j}\right)+\alpha\left[r^{j}+\gamma v_{t}^{j}\left(s^{\prime}\right)\right]\) \(v_{t}^{j}\left(s^{\prime}\right)=\sum_{a^{j}} \pi_{t}^{j}\left(a^{j} | s^{\prime}, \bar{a}_{1}^{j}, \ldots \bar{a}_{M}^{j}\right) \mathbb{E}_{a_{i}^{-j} \sim \pi_{t}^{-j}}\left[Q_{t}^{j}\left[s^{\prime}, a^{j}, \bar{a}_{1}^{j}, \ldots \bar{a}_{M}^{j}\right]\right]\) \(\bar{a}_{i}^{j}=\frac{1}{N_{i}^{j}} \sum_{k} a_{i}^{k}, a_{i}^{k} \sim \pi_{t}^{k}\left(\cdot | s, \bar{a}_{1-}^{k}, \ldots, \bar{a}_{M-}^{k}\right)\) \(\pi_{t}^{j}\left(a^{j} | s, \bar{a}_{1}^{j}, \ldots \bar{a}_{M}^{j}\right)=\frac{\exp \left(\beta Q_{t}^{j}\left(s, a^{j}, \bar{a}_{1}^{j}, \ldots, \bar{a}_{M}^{j}\right)\right)}{\sum_{a j^{\prime} \in A^{j}} \exp \left(\beta Q_{t}^{j}\left(s, a^{\prime}, \bar{a}_{1}^{j}, \ldots \bar{a}_{M}^{j}\right)\right)}\)
文中给出了证明,证明该更新方式可收敛到距离纳什均衡有限距离内的固定点。
2.3 算法流程


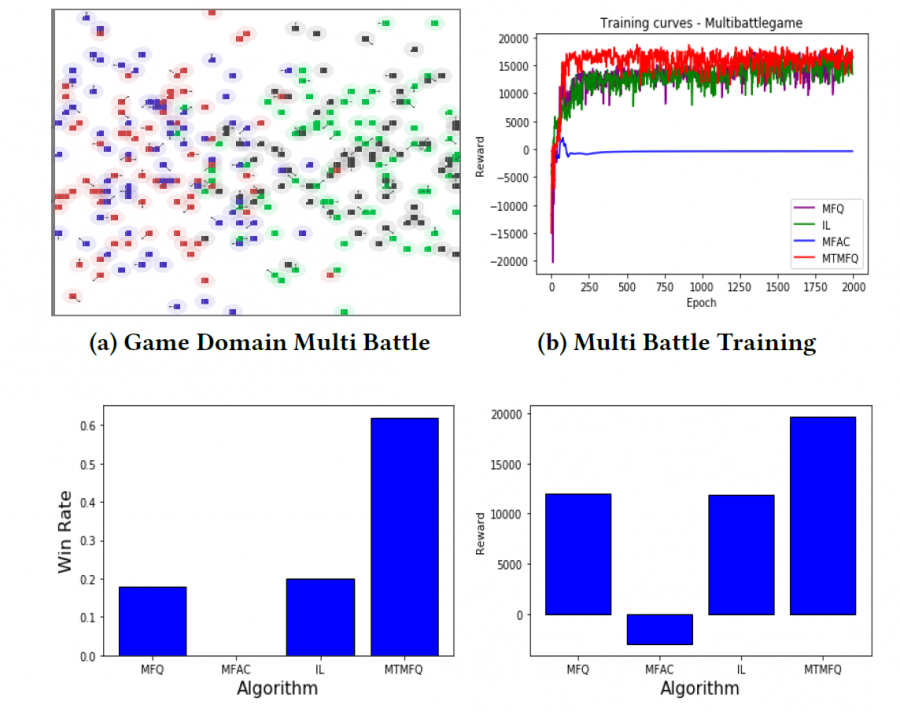
三、实验内容
在MAgent上实验。效果超过了MFQ与MFAC:
四、缺点
计算非常复杂。
五、优点
完善了Mean Field理论在多智能体中的应用。
您的打赏是对我最大的鼓励!
 支付宝打赏
支付宝打赏  微信打赏
微信打赏