1. 简介
当问题具有下列特性时,通常可以考虑使用动态规划来求解:
- 第一个特性是一个复杂问题的最优解由数个小问题的最优解构成,可以通过寻找子问题的最优解来得到复杂问题的最优解;
- 子问题在复杂问题内重复出现,使得子问题的解可以被存储起来重复利用。
马尔可夫决策过程(MDP)具有上述两个属性:Bellman方程把问题递归为求解子问题,价值函数就相当于存储了一些子问题的解,可以复用。因此可以使用动态规划来求解MDP。
我们用动态规划算法来求解一类称为“规划 Planning”的问题。“规划”指的是在了解整个MDP的基础上求解最优策略,也就是清楚模型结构的基础上:包括状态行为空间、转换矩阵、奖励等。这类问题不是典型的强化学习问题,我们可以用规划来解决Predict和Control问题。

2. 策略迭代 Policy Iteration
2.1 方法简介
这个方法主要分为两步:
- Policy Evaluation:基于当前的Policy计算出每个状态的value function $V$(迭代计算直到收敛)。
- Policy Improvment:基于当前的value function,采用贪心算法来找到当前最优的Policy $\pi$。
如此反复多次,最终得到最优策略$\pi^{*}$ 和最优状态价值函数$V^{*}$:
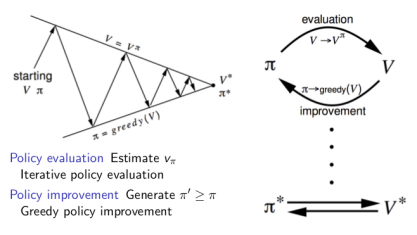
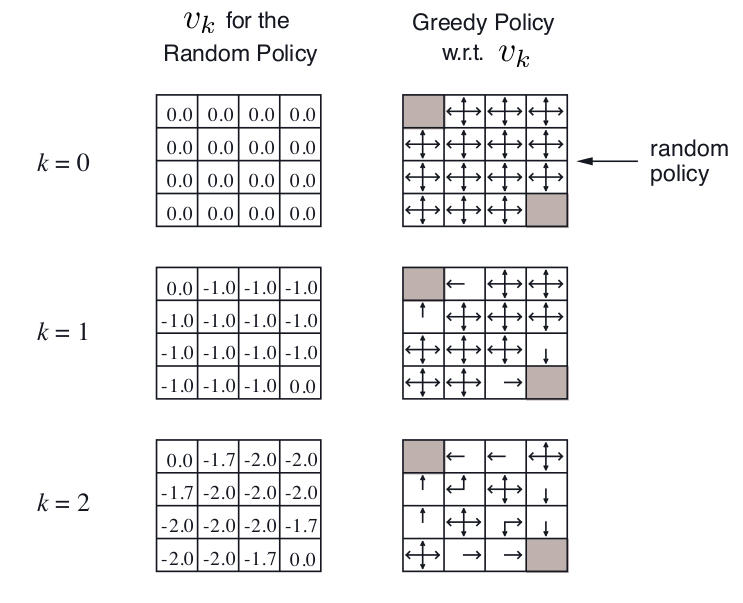
下图是一个叫Small Gridworld的例子,左上角和右下角是终点,$\gamma=1$,移动一步reward=-1,起始的random policy是朝每个能走的方向概率相同。
2.2 方法证明
2.2.1 Policy Evaluation收敛性证明
2.2.1.1 压缩映射
定义: 对于一个度量空间$\langle M, d\rangle$,和一个函数映射$f : M \mapsto M$, 如果存在实数$k \in[0,1)$, 使得对于$M$中的任意两个点$x,y$,满足$d(f(x), f(y)) \leq k d(x, y)$,那么就称$f$是该度量空间中的一个压缩映射,其中满足条件的最小的$k$值称为Lipschitz常数。
2.2.1.2 压缩映射定理
对于完备的度量空间$\langle M, d\rangle$,如果$f : M \mapsto M$是它的一个压缩映射,那么
- 在该度量空间中,存在唯一的点$x_{*}$满足$f\left(x_{*}\right)=x_{*}$。
- 并且,对于任意的$x \in M$, 定义序列$f^{2}(x)=f(f(x)), f^{3}(x)=f\left(f^{2}(x)\right) |, \cdots,f^{n}(x)=f\left(f^{n-1}(x)\right)$,该序列会收敛于$x_{*}$,即$\lim_{n \rightarrow \infty} f^{n}(x)=x_{*}$
结论:完备度量空间上的压缩映射具有唯一的不动点。从度量空间任何一点出发,只要满足压缩映射,压缩映射的序列必定会收敛到唯一的不动点。因此证明一个迭代序列是不是收敛,只要证明该序列所对应的映射是不是压缩映射。
2.2.1.3 贝尔曼期望方程及其向量形式
贝尔曼期望方程为:\(v_{\pi}(s)=\sum_{a \in A} \pi(a | s)\left(R_{s}^{a}+\gamma \sum_{s^{\prime} \in S} P_{s s^{\prime}}^{a} v_{\pi}\left(s^{\prime}\right)\right) \tag1\)
可进一步拆解为\(v_{\pi}(s)=\sum_{a \in A} \pi(a \| s)R_{s}^{a}+\sum_{a \in A} \pi(a \| s)\gamma \sum_{s^{\prime} \in S} P_{s s^{\prime}}^{a} v_{\pi}\left(s^{\prime}\right) \tag2\)
如图所示:
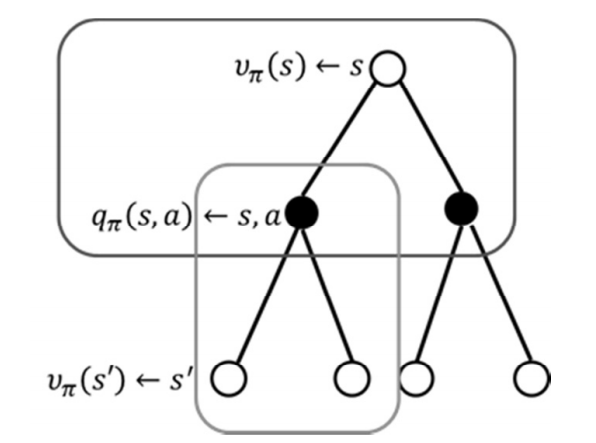
接下来将它写为向量矩阵形式。因为状态是有限的,设状态集合为
\[S=\left\{S_{0}, S_{1}, \ldots, S_{n}\right\}\]状态价值矩阵为
\[V_{\pi}=\left\{V_{\pi}\left(s_{0}\right), V_{\pi}\left(s_{1}\right), \cdots, V_{\pi}\left(s_{n}\right)\right\}^{T}\]计算状态价值函数所用的概率矩阵为:
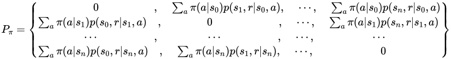
收益矩阵为
\[R_{\pi}=\left\{R_{0}, R_{1}, \cdots, R_{n}\right\}^{T}\]由公式(2)前半部分可知,在当前状态、动作、新状态确定的情况下, $R_{\pi}$也是确定的,为常数矩阵
所以所有状态的价值函数用矩阵形式表示为:
\[V_{\pi}=R_{\pi}+\gamma P_{\pi} V_{\pi} \tag3\]2.2.1.4 收敛性证明
从当前值函数到下一个迭代值函数的映射可表示为:
\[T_{\pi}(v)=R_{\pi}+\gamma P_{\pi} v\]证明为压缩映射:
\[\begin{equation} \begin{aligned} &\rho\left(T_{\pi}(u), T_{\pi}(v)\right) =\left|T_{\pi}(u)-T_{\pi}(v)\right|_{\infty} \\ &=\left|\left(R_{\pi}+\gamma P_{\pi} u\right)-\left(R_{\pi}+\gamma P_{\pi} v\right)\right|_{\infty} \\ &=\left|\gamma P_{\pi}(u-v)\right|_{\infty} \\ & \leqslant\left|\gamma P_{\pi}\right| u-v\left|_{\infty}\right|_{\infty} \\ & \leqslant \gamma\|u-v\|_{\infty} \end{aligned} \end{equation}\]根据压缩映射定理:贝尔曼期望方程收敛于唯一的$v_{\pi}$;迭代式策略评价算法以$\gamma$的线性速率收敛于$v_{\pi}$。
2.2.2 Policy Improvement收敛性和最优性证明
我们可以通过单调递增来证明。
假设我们有一个确定性的策略$a=\pi(s)$,那么我们可以通过贪心地选择动作来改进策略:
\[\pi^{\prime}(s)=\underset{a \in \mathcal{A}}{\operatorname{argmax}} q_{\pi}(s, a)\]这样贪婪的策略可以保证提升一步后的动作值函数:
\[q_{\pi}\left(s, \pi^{\prime}(s)\right)=\max_{a \in \mathcal{A}} q_{\pi}(s, a) \geq q_{\pi}(s, \pi(s))=v_{\pi}(s)\]因此可以保证提升值函数:
\[\begin{aligned} v_{\pi}(s) & \leq q_{\pi}\left(s, \pi^{\prime}(s)\right)=\mathbb{E}\left[R_{t+1}+\gamma v_{\pi}\left(S_{t+1}\right) | S_{t}=s,A_{t}=\pi'(s)\right] \\\ & = \mathbb{E}_{\pi^{\prime}}\left[R_{t+1}+\gamma v_{\pi}\left(S_{t+1}\right) | S_{t}=s\right] \\\ & \leq \mathbb{E}_{\pi^{\prime}}\left[R_{t+1}+\gamma q_{\pi}\left(S_{t+1}, \pi^{\prime}\left(S_{t+1}\right)\right) | S_{t}=s\right] \\\ & \leq \mathbb{E}_{\pi^{\prime}}\left[R_{t+1}+\gamma R_{t+2}+\gamma^{2} q_{\pi}\left(S_{t+2}, \pi^{\prime}\left(S_{t+2}\right)\right) | S_{t}=s\right] \\\ & \leq \mathbb{E}_{\pi^{\prime}}\left[R_{t+1}+\gamma R_{t+2}+\ldots | S_{t}=s\right]=v_{\pi^{\prime}}(s) \end{aligned}\]由于状态空间和动作空间是有限的,我们一定可以遍历所有<状态,动作>对。当遍历结束之后,即改进停止时,我们可以满足如下条件:\(q_{\pi}\left(s, \pi^{\prime}(s)\right)=\max_{a \in \mathcal{A}} q_{\pi}(s, a)=q_{\pi}(s, \pi(s))=v_{\pi}(s)\)
此时已经满足贝尔曼最优方程:
\[v_{\pi}(s)=\max_{a \in \mathcal{A}} q_{\pi}(s, a)\]此时,对于所有状态来说$V_{\pi}(s)=v_{*}(s)$,即$\pi$就是最优策略。
对应$\epsilon$-greedy Policy Improvement来说,假设$m$个动作都以非零的$\epsilon/m$的概率被探索,$1-\epsilon$的概率选择贪心动作,那么
\[\pi(a | s)=\left\{\begin{array}{ll}{\epsilon / m+1-\epsilon} & {\text { if } a^{*}=\underset{a \in \mathcal{A}}{\operatorname{argmax}} Q(s, a)} \\ {\epsilon / m} & {\text { otherwise }}\end{array}\right.\]对于任意一个$\epsilon$-greedy的策略$\pi$来说,可证基于$q_{\pi}$的$\epsilon$-greedy的策略$\pi’$,$v_{\pi^{\prime}}(s) \geq v_{\pi}(s)$:
\[\begin{aligned} q_{\pi}\left(s, \pi^{\prime}(s)\right) &=\sum_{a \in \mathcal{A}} \pi^{\prime}(a | s) q_{\pi}(s, a) \\\ &=\epsilon / m \sum q_{\pi}(s, a)+(1-\epsilon) \max_{a \in \mathcal{A}} q_{\pi}(s, a) \\\ & \geq \epsilon / m \sum_{a \in \mathcal{A}} q_{\pi}(s, a)+(1-\epsilon) \sum_{a \in \mathcal{A}} \frac{\pi(a | s)-\epsilon / m}{1-\epsilon} q_{\pi}(s, a) \\\ &=\sum_{a \in \mathcal{A}} \pi(a | s) q_{\pi}(s, a)=v_{\pi}(s) \end{aligned}\]因此,根据policy improvement theorem,$v_{\pi^{\prime}}(s) \geq v_{\pi}(s)$
3. 值迭代 Value Iteration
3.1 优化原则 Principle of Optimality
一个最优策略可以被分解为两部分:从状态$s$到下一个状态$s’$采取了最优行为$A_{*}$;在状态$s’$时遵循一个最优策略。

3.2 方法简介
从上面原理出发,如果已知子问题的最优值$v_{∗}(s’)$,那么就能通过第一个Bellman Optimality Equation将 $v_{∗}(s)$也推出来。
\[v_{*}(s) \leftarrow \max _{a \in \mathcal{A}} \mathcal{R}_{s}^{*}+\gamma \sum_{s^{\prime} \in \mathcal{S}} \mathcal{P}_{\mathrm{ss}^{\prime}}^{4} v_{*}\left(s^{\prime}\right)\]因此从终点开始向起点推就能把全部状态最优值推出来。
Value Iteration通过迭代的方法,通过这一步的$v_{k}(s’)$更新下一步的$v_{k+1}(s)$,最终收敛到最优的$v_{∗}$,需要注意的是中间生成的value function的值不对应着任何policy。
考虑下面这个Shortest Path例子,左上角是终点,要求的是剩下每一个格子距离终点的最短距离,每走一步,reward=-1。
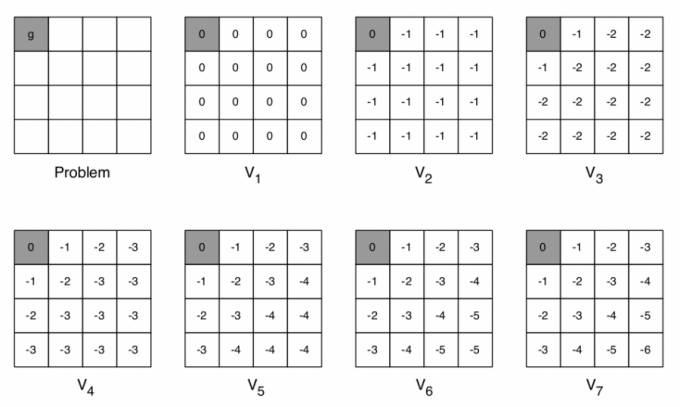
4. PI与VI的缺陷
在实际中PI与VI存在一定的缺陷:
- 无法处理连续状态与动作空间
- 当状态空间巨大时存在维度诅咒的问题
- 不适用与POMDP
- 使用动态规划的方式要求知道状态转移概率与奖励,但在实际中往往无法获得
5. 总结
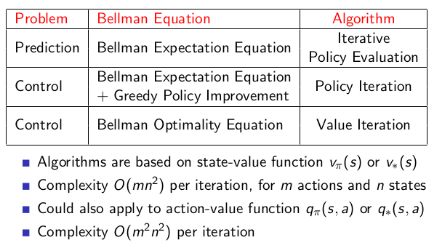
因此,针对MDP要解决的两个问题,有如下几种方式来解决。针对prediction,因为它的目标是在已知的Policy下得到收敛的value function,因此针对问题不断迭代计算Bellman Expectation Equation就够了,但是control则需要同时获得最优的policy,那么在Iterative Policy Evaluation的基础上加入一个选择Policy的过程就行了,也就是上面的Policy Iteration,另外Value Iteration虽然在迭代的过程中没有显式计算出policy,但是在得到最优的value function之后就能推导出最优的policy,因此也能用做解决control问题。
您的打赏是对我最大的鼓励!
 支付宝打赏
支付宝打赏  微信打赏
微信打赏