一、问题
VDN将联合动作价值函数分解为单个动作价值函数的和。QMIX扩展了这种可加性的值函数,进行因子分解,将联合作用价值函数表示为单调函数,而不是仅仅为加和,从而实现了环境的更进一步扩展。这些方法里具有很多限制结构,经常遇到不能分解的任务。
本文的ideal是:如果联合行动价值函数的最优行动与单个行动价值函数的最优行动相同,则任务是可因式分解的。
本文采用一种新方法QTRAN将原来的联合行动价值函数转换为一种易于分解的函数,它们具有相同的最优行动,这种方法有更一般的降解,适合更多的场合,号称可以降解一切可以降解任务。
二、解法
2.1 背景
2.1.1 Decentralized POMDP
Decentralized POMDP是用来给合作式多智能体任务建模的标准方法,简称DEC-POMDP,表示为$\mathcal{G}=<\mathcal{S}, \mathcal{U}, P, r, \mathcal{Z}, O, N, \gamma>$:
- $i \in N:={1,…,N}$:N个agents.
- $s \in S$:环境的真实状态
- $u_{i} \in U$:每个agent的动作
- $u:=\left[u_{i}\right]_{i=1}^{N} \in \mathcal{U}^{N}$:联合动作向量
- $P\left(s^{\prime} | s, u\right): \mathcal{S} \times \mathcal{U}^{N} \times \mathcal{S} \mapsto[0,1]$:状态转移方程
- $r(s, u): \mathcal{S} \times \mathcal{U}^{N} \mapsto \mathbb{R}$:共享的联合奖励函数
- $\gamma \in[0,1)$:折扣因子
- $z = O(s, i): \mathcal{S} \times \mathcal{N} \mapsto \mathcal{Z}$:每个agent自己的部分观察
- $\tau_{i} \in \mathcal{T}:=(\mathcal{Z} \times \mathcal{U})^{*}$:每个agent的动作-观察历史
2.1.2 IGM Condition and Factorizable Task
下面给出IGM与可分解任务的定义。IGM全称Individual-Global-Max,可以理解为独立值函数最大化与联合值函数最大化的一致性,具体定义为;
给定一个联合动作值函数$Q_{\mathrm{jt}}: \mathcal{T}^{N} \times \mathcal{U}^{N} \mapsto \mathbb{R}$,其中$\tau \in \mathcal{T}^{N}$是联合动作-观察历史,如果存在一系列的独立动作值函数$\left[Q_{i}: \mathcal{T} \times \mathcal{U} \mapsto \mathbb{R}\right]_{i=1}^{N}$使得如下条件成立:
\[\arg \max _{\boldsymbol{u}} Q_{\text {jt }}(\boldsymbol{\tau}, \boldsymbol{u})=\left(\begin{array}{c} \arg \max _{u_{1}} Q_{1}\left(\tau_{1}, u_{1}\right) \\ \vdots \\ \arg \max _{u_{N}} Q_{N}\left(\tau_{n}, u_{N}\right) \end{array}\right)\]则认为$\left[Q_{i}\right]$对于$Q_{\mathrm{jt}}$满足IGM,即$Q_{\mathrm{jt}}(\tau, \boldsymbol{u})$可以被$\left[Q_{i}\left(\tau_{i}, u_{i}\right)\right]$分解。
如果某任务的$Q_{\mathrm{jt}}(\tau, \boldsymbol{u})$对于所有的$\tau \in \mathcal{T}^{N}$都可分解,那么就认为该任务本身是可分解的。
VDN和QMIX的分解方式其实本质上是满足IGM的充分非必要条件:
\[\begin{aligned} &\text { (Additivity) } \quad Q_{\mathrm{jt}}(\tau, u)=\sum_{i=1}^{N} Q_{i}\left(\tau_{i}, u_{i}\right)\\ &\text { (Monotonicity) } \frac{\partial Q_{\text {jt }}(\tau, u)}{\partial Q_{i}\left(\tau_{i}, u_{i}\right)} \geq 0, \quad \forall i \in \mathcal{N} \end{aligned}\]它们与本文QTRAN方法的关系可以用下图表示:
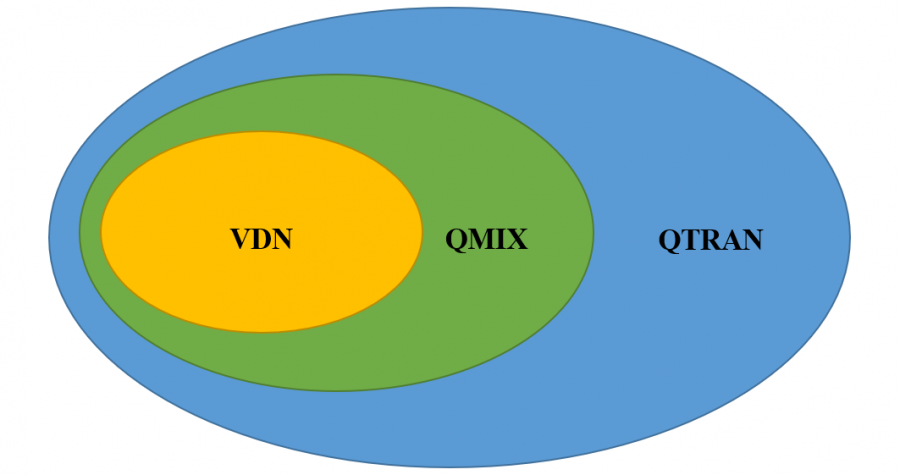
2.2 QTRAN
QTRAN核心思想是将原有的联合行动价值函数$Q_{\mathrm{jt}}(\tau, u)$转换为与$Q_{\mathrm{jt}}(\tau, u)$共享最优联合行动的$Q^{‘}_{\mathrm{jt}}(\tau, u)$
2.2.1 可分解值函数
可分解值函数的特点由如下定理给出:
Theorem 1:令$\overline{\boldsymbol{u}}_{i}=\arg \max_{u_{i}} Q_{i}\left(\tau_{i}, u_{i}\right)$为最优的局部动作,$\overline{\boldsymbol{u}}=\left[\bar{u}_{i}\right]_{i=1}^{N}$,当满足以下条件时,一个可分解的联合动作值函数$Q_{\text {jt }}(\tau, \boldsymbol{u})$可分解为$\left[Q_{i}\left(\tau_{i}, u_{i}\right)\right]$:
\[\sum_{i=1}^{N} Q_{i}\left(\tau_{i}, u_{i}\right)-Q_{\mathrm{jt}}(\tau, u)+V_{\mathrm{jt}}(\tau)=\left\{\begin{array}{ll} 0 & u=\bar{u}, \\ \geq 0 & u \neq \bar{u} \end{array}\right.\]其中
\[V_{\mathrm{jt}}(\tau)=\max _{u} Q_{\mathrm{jt}}(\tau, u)-\sum_{i=1}^{N} Q_{i}\left(\tau_{i}, \bar{u}_{i}\right)\]证明如下:
\[\begin{aligned} Q_{\mathrm{jt}}(\tau, \bar{u}) &=\sum_{i=1}^{N} Q_{i}\left(\tau_{i}, \bar{u}_{i}\right)+V_{\mathrm{jt}}(\tau) \quad(\text { From }(4 \mathrm{a})) \\ & \geq \sum_{i=1}^{N} Q_{i}\left(\tau_{i}, u_{i}\right)+V_{\mathrm{jt}}(\tau) \\ & \geq Q_{\mathrm{jt}}(\tau, u) \quad(\text { From }(4 \mathrm{b})) \end{aligned}\]注意,对于映射变化$\phi(\boldsymbol{Q})=A \cdot \boldsymbol{Q}+B$来说,如果$A=\left[a_{ii} \right] \in \mathbb{R}_{+}^{N \times N}$是对称的对角矩阵且$a_{i i}>0, \forall i$,$B=\left[b_{i}\right] \in \mathbb{R}^{N}$,那么上述定理依旧成立。可以把$A$与$B$看作是缩放与偏差。
因此可以找到一个转换联合动作值函数$Q^{‘}_{\mathrm{jt}}(\tau, u)$满足上述定理:
\[Q_{\mathrm{jt}}^{\prime}(\tau, u):=\sum_{i=1}^{N} Q_{i}\left(\tau_{i}, u_{i}\right)\]这是因为这种加和形式下,$\left[Q_{i}\right]$对于$Q_{\mathrm{jt}}^{\prime}$满足IGM,又因为$\arg \max_{\boldsymbol{u}} Q_{\text {jt }}(\boldsymbol{\tau}, \boldsymbol{u})=\arg \max_{\boldsymbol{u}} Q_{\text {jt }}^{\prime}(\boldsymbol{\tau}, \boldsymbol{u})$,所以$\left[Q_{i}\right]$就是$Q_{\mathrm{jt}}^{\prime}$的分解。
2.2.2 方法框架
QTRAN的框架如下图所示:
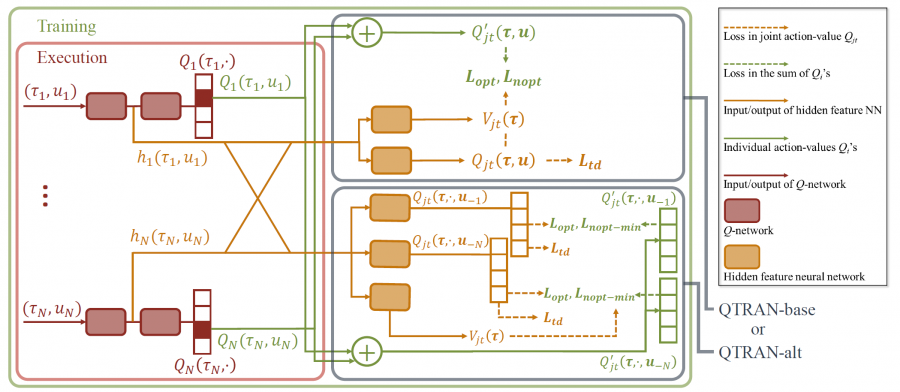
其中包含三个网络:
\[\begin{aligned} &\text{独立动作值函数网络:}f_{\mathbf{q}}:\left(\tau_{i}, u_{i}\right) \mapsto Q_{i}\\ &\text{联合动作值函数网络:}f_{\mathrm{r}}:(\tau, \boldsymbol{u}) \mapsto Q_{\mathrm{jt}}\\ &\text{状态值函数网络:}f_{\mathbf{v}}: \boldsymbol{\tau} \mapsto V_{j t} \end{aligned}\]其中,联合动作值函数网络使用所有独立动作值函数网络采样得到的动作进行更新,并连接各个所有独立动作值函数网络底层输出的隐性特征$h_{i}\left(\tau_{i}, u_{i}\right)=\left[h_{Q, i}\left(\tau_{i}, u_{i}\right), h_{V, i}\left(\tau_{i}\right)\right]$
2.2.3 损失函数
QTRAN中的loss函数由三部分组成:
\[L\left(\boldsymbol{\tau}, \boldsymbol{u}, \boldsymbol{r}, \boldsymbol{\tau}^{\prime} ; \boldsymbol{\theta}\right)=L_{\mathrm{td}}+\lambda_{\mathrm{opt}} L_{\mathrm{opt}}+\lambda_{\mathrm{nopt}} L_{\mathrm{nopt}}\]其中:$L_{\mathrm{td}}$用于评估真实的动作值,$ L_{\mathrm{opt}}$和$L_{\mathrm{nopt}}$用于评估分解$Q_{jt}$为$\left[Q_{i}\right]$时是否满足Theorem 1。由于Theorem 1的条件需要在训练中采样大量样本才能满足,这里做了简化,即在训练$ L_{\mathrm{opt}}$和$L_{\mathrm{nopt}}$时固定$Q_{jt}$,并使用$\hat{Q}_{\mathrm{jt}}$来表示这个固定的$Q_{jt}$。具体每个损失函数的定义如下:
\[\begin{aligned} L_{\mathrm{td}}(; \boldsymbol{\theta}) &=\left(Q_{\mathrm{jt}}(\tau, \boldsymbol{u})-y^{\mathrm{d} \mathrm{q} \mathrm{n}}\left(r, \boldsymbol{\tau}^{\prime} ; \boldsymbol{\theta}^{-}\right)\right)^{2} \\ L_{\mathrm{opt}}(; \boldsymbol{\theta}) &=\left(Q_{\mathrm{jt}}^{\prime}(\tau, \overline{\boldsymbol{u}})-\hat{Q}_{\mathrm{jt}}(\tau, \overline{\boldsymbol{u}})+V_{\mathrm{jt}}(\tau)\right)^{2} \\ L_{\mathrm{nopt}}(; \boldsymbol{\theta}) &=\left(\min \left[Q_{\mathrm{jt}}^{\prime}(\tau, \boldsymbol{u})-\hat{Q}_{\mathrm{jt}}(\tau, \boldsymbol{u})+V_{\mathrm{jt}}(\tau), 0\right]\right)^{2} \end{aligned}\]其中$y^{\mathrm{dqn}}\left(r, \boldsymbol{\tau}^{\prime} ; \boldsymbol{\theta}^{-}\right)=r+\gamma Q_{\mathrm{jt}}\left(\tau^{\prime}, \overline{\boldsymbol{u}}^{\prime} ; \boldsymbol{\theta}^{-}\right)$,$\bar{u}^{\prime}=\left[\arg \max_{u_{1}} Q_{i}\left(\tau_{i}^{\prime}, u_{i} ; \boldsymbol{\theta}^{-}\right)\right]_{i-1}^{N}$,$\theta^{-}$为DQN目标网络的参数。
2.2.4 修改对联合行动价值函数的追踪
上述版本的QTRAN称为QTRAN-base,反映其如何追踪联合行动价值函数的基本性质。然而,Theorem 1的第二个条件太宽,导致神经网络无法完成构建$Q_{jt}$正确的分解,即对非最优行为施加不良影响,这进而影响了训练过程的稳定性和收敛速度。这促使去研究比Theorem 1的第二个条件更强的条件,同时满足Theorem 1的仿射变换的不变性:
Theorem 2:Theorem 1的第二个条件替换为如下条件时,Theorem 1依旧成立。当$u=\bar{u}$时,
\[\begin{aligned} \min_{u_{i} \in \mathcal{U}}[& Q_{\mathrm{jt}}^{\prime}\left(\tau, u_{i}, \boldsymbol{u}_{-i}\right)-Q_{\mathrm{jt}}\left(\tau, u_{i}, \boldsymbol{u}_{-i}\right) + \left.V_{\mathrm{jt}}(\tau)\right]=0, \quad \forall i=1, \ldots, N \end{aligned}\]其中$\boldsymbol{u}_{-i}=\left(u_{1}, \ldots, u_{i-1}, u_{i+1}, \ldots, u_{N}\right)$,即除了agent $i$以外的所有动作。
为了实现Theorem 2,使用反事实联合网络来替代联合动作值函数网络,即对于每个agent都设置一个反事实网络$Q_{\mathrm{jt}}\left(\tau, \cdot, \boldsymbol{u}_{-i}\right)$。同时将$L_{\text {nopt }}$替换为$L_{\text {nopt-min }}$:
\[L_{\mathrm{nopt}-\min }\left(\tau, u, r, \tau^{\prime} ; \theta\right)=\frac{1}{N} \sum_{i=1}^{N}\left(\min _{u_{i} \in U} D\left(\tau, u_{i}, u_{-i}\right)\right)^{2}\]其中$D\left(\tau, u_{i}, u_{-i}\right)=Q_{\mathrm{jt}}^{\prime}\left(\tau, u_{i}, u_{-i}\right)-\hat{Q}_{\mathrm{jt}}\left(\tau, u_{i}, u_{-i}\right)+V_{\mathrm{jt}}(\tau)$
三、实验内容
在下图的单状态马尔科夫博弈中,QTRAN是唯一获得最优解的:
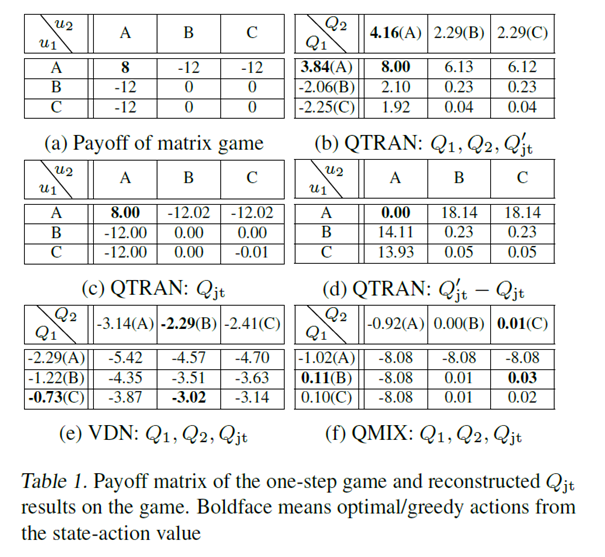
QTRAN-alt比QTRAN-base更好地区分最优动作与非最优动作:
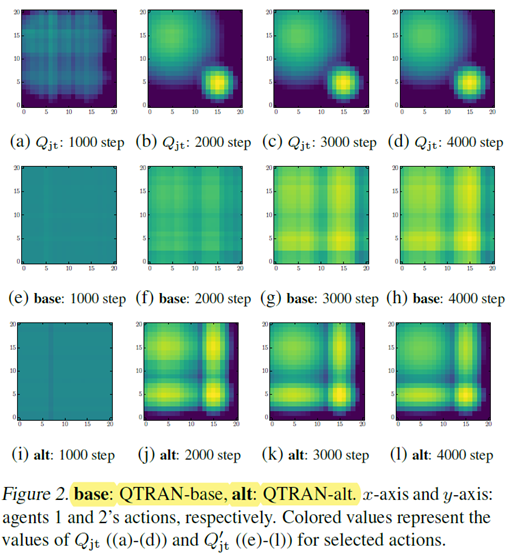
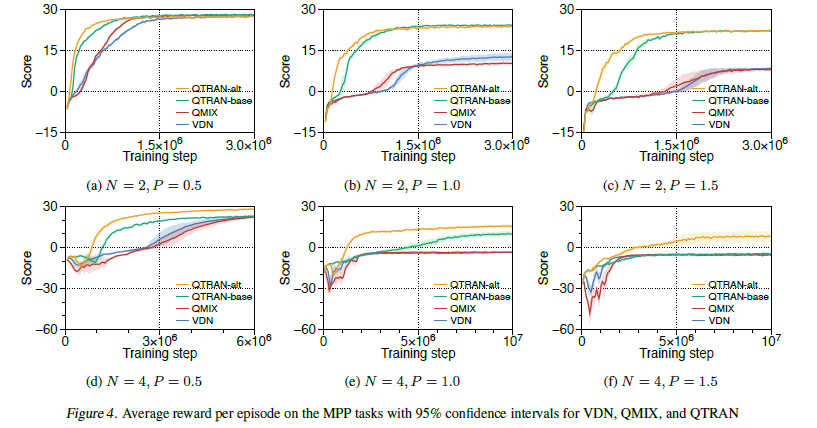
将Multi-domain Gaussian Squeeze、Modified predator-prey等环境设置为强迫合作式的环境,表现超越了VDN与QMIX:
四、缺点
-
分解的Q值依旧没有实际含义
-
在复杂的MARL任务上的实际表现很差,因为由于QTRAN使用的约束太过松散,实现时的过多近似会导致在很多任务上效果不如Q-mix理想
五、优点
- 进一步扩大了Q值分解理论的适用范围
- 采用类似dueling network的结构可以提升学习效果, 加速收敛。
您的打赏是对我最大的鼓励!
 支付宝打赏
支付宝打赏  微信打赏
微信打赏